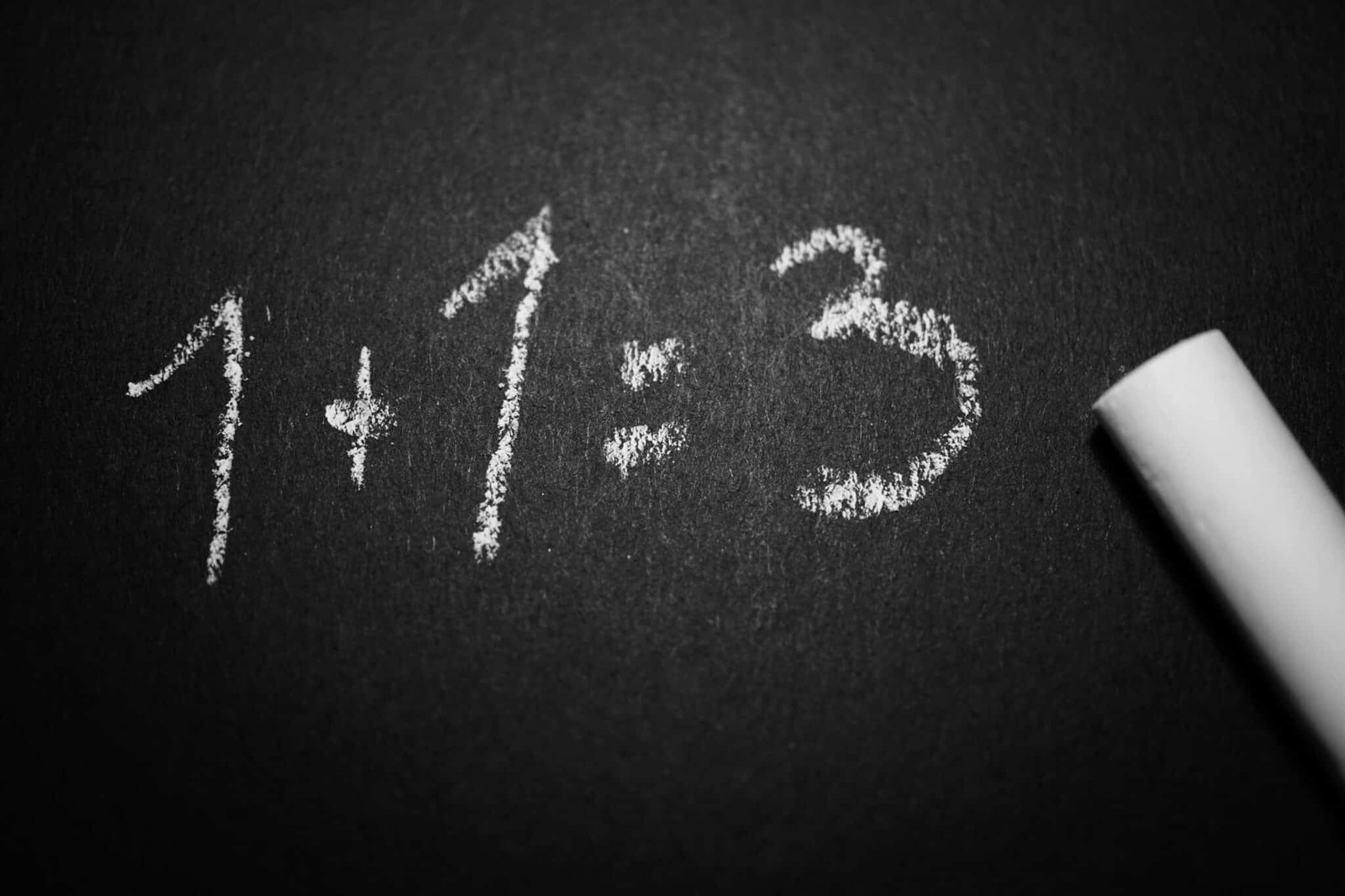A whole number fraction brings fun and practicality to math! Furthermore, they combine whole numbers and fractions. Furthermore, they make calculations engaging and relatable. You can use fraction from splitting pizzas to measuring ingredients. They are the most practical mathematical concepts. Therefore, you must master them to unlock creative problem-solving skills. You can turn math challenges into exciting opportunities.
A Brief History of Whole Number Fractions
Whole number fractions have roots in ancient civilizations like Egypt and Mesopotamia. Moreover, the early scholars used fractions for trade, astronomy, and construction. However, over time, Greek mathematicians standardized fraction notation. In addition, they also enhanced mathematical clarity. Later, during the Middle Ages, Arabic scholars preserved and expanded the methods. In short, they created foundations for modern-day fractions.
European mathematicians refined fraction systems in the Renaissance period. They further introduced decimal equivalents to the whole number fraction. In addition, the printing presses promoted the advancements. Moreover, the scholars revolutionized education and trade. Consequently, the fraction became integral to science and commerce.
Today, the fraction system is essential for various applications. The fractions highlight the importance in mathematics, technology, and every day problem-solving.
Different forms of whole number fractions
Proper Fractions
The first from of whole number fraction has numerators smaller than their denominators. For example, 2/5 . Moreover, they represent parts of a whole. Lastly, you can convert them easily into decimals or percentages.
Improper Fractions
The second fraction is called an improper fraction. The fraction has a bigger numerator than the denominator. You can easily convert an improper whole number fraction into mixed numbers.
Mixed Numbers
Thirdly, you can combine whole numbers with proper fractions. In short, they visually show whole parts and remainders. In addition, their composition helps during interpretation.
Equivalent Fractions
Despite having different numerators and denominators, equivalent whole number fractions do exist. Some fractions represent the same value. They simplify calculations when reducing fractions.
Unit Fractions
The final form of fractions has a numerator of one. Some fractions form the building blocks for other fractions.
Whole Number Fraction 1: 2/5 + ¾
The first whole number fraction is straightforward. In other words, there are no whole numbers. You have only pure fractions. So, let’s solve it together:
Step 1: Multiply the denominators of whole number fraction
Foremost, we mention the denominators 5 and 4. Next, we multiply and team them up.
Therefore, 5×4=205. Now, this becomes the common denominator.
Step 2: Cross multiplies for the numerators.
Imagine the fractions crisscrossing! Secondly, we multiply each number with the opposing position of the same number.
- 2×4=8. So, the numerator of
2/5 crosses to meet 4.
- 3×5=15. So, the numerator of ¾ meets 5 of the first fraction.
Step 3: Add the numerators
Thirdly, we add 8+15=23. Therefore, this is your new numerator.
Step 4: Write the whole number fraction
First, write the denominator from Step 1. It is 20.
Lastly, write the numerator from Step 3. It is 23.
The final answer is 23/20. In other words, the mixed fraction is 1 3/20
Whole Number Fraction Two: 3+ 5/2
Here’s where we mix things up! The subsequent whole number fraction contains two elements.
Step 1: Multiply the denominators
Foremost, the whole number 3. However, it is secretly 3/1 . In other words, one is hiding in the fraction side. therefore, we multiply 1×2=2. Thus, the common denominator becomes two.
Step 2: Cross multiply the whole number fraction
Just like before, we crisscross the numbers to solve the whole number fraction:
First, 3×2=6. In other words, the whole numbers come together with the fraction’s denominator. Next, we multiply 5×1=5. As a result, the numerator of greets the whole number’s denominator.
Step 3: Add the results
Thirdly, we combine 6+5=11. Now, greet our new numerator.
Step 4: Write the fraction.
First, write the denominator 2 from Step 1 underneath the fraction. Lastly, write the numerator 11 from Step 3 above the fraction. Therefore, the final whole number fraction is 11/2 or 5 1/2
Whole Number Fraction Three: 2 1/3 + 3 2/5
It is time to level up! Now, we work with mixed whole number fractions! Foremost, the solution requires you to convert the whole fractions into improper fractions first.
Step 1: Multiply the denominators
The denominators are 3 and 5. Therefore, you will multiply them together: 3×5=15. Now, you have our common denominator.
Step 2: Convert the mixed numbers into improper fractions
Here’s how:
For 2 1/3, you will multiply 2 and the denominator 3. Next, we add the numerator 1. In short, the new numerator is 2×3+1=7. Thus, the new fraction is .
Secondly, we solve for 3 2/5 . First, multiply the whole number 3 and the denominator 5. Subsequently, add the numerator 2 to the initial result. In other words, 3×5+2=17. Now, the new fraction is .
Step 3: Write the improper fractions separately.
The new fractions are 17 /5 and 7/3.
Step 4: Cross multiply
First, 7 and 5 become 35. Subsequently, you multiple 17 to 3 to make it 51.
Step 5: Add the numerators
Next, add 35+51=86.
Step 6: Write the new whole number fraction.
Are you ready to discover the new whole number fraction? The new denominator is 15. And, the numerator is 86. You can revisit step 1 and 5 for clarity. Therefore, the final answer is 86/15 or 5 11/15
Whole Number Fraction Four: 3 1/5 + 4 2/3
We present another fraction problem! However, we will tackle it with ease!
Step 1: Multiply the denominators.
Firstly, we multiply the denominators 5 and 3. Now, the new denominator is 15.
Step 2: Convert the mixed numbers into improper fractions.
For 3 1/5, we multiply 3×5+1=16. As a result, the new first whole number fraction is 16/5.
For 4 2/3, you will multiply 4×3+2=14. Now, the second fraction is 14/3.
Step 3: Write the improper fractions separately
The two subsequent whole number fractions that you successfully converted are 16/5 and 14/3.
Step 4: You Cross multiply.
16×3=48 and 16 ×3=48.
Step 5: Add the numerators.
Now, you combine 48+70=118.
Step 6: Write the fraction
Lastly, the denominator is 15 and the new numerator is 118. However, you can visit steps 1 and 5 for more clarity.
The final answer is 118/15. In other words, the mixed fraction is 7 13/15.
Tips for Solving Whole Number Fractions in a Math Test

Read the whole number fraction question carefully
First, you must understand what the whole number fraction problem is asking.
Convert mixed numbers:
Next, you must change the mixed to improper fractions for easier calculations.
Find a common denominator of the whole number fraction
Subsequently, you must simplify addition or subtraction by aligning denominators.
Check your work
Finally, you must review each step to avoid calculation errors.
Practice time management
Lastly, you must allocate enough time per whole number proper question to finish on time.
Solve a whole number fraction with our help!
Thanks for reading! We hope the lesson on fractions was insightful. Stay tuned for more product reviews. You can shop for school supplies here to prepare for your next math test.