Math Olympiad questions require an effective preparation plan as the competition is fast approaching. Success demands sharp problem-solving skills, quick thinking, and, also, strategic practice. Therefore, you must follow a structured approach. As a result, you can maximize efficiency and enhance performance. Staying disciplined and applying key strategies will help you tackle even the toughest problems confidently.
What is the Math Olympiad?
The Math Olympiad is an elite competition that tests students’ problem-solving abilities. Participants face complex questions requiring logical reasoning and creative thinking. Therefore, you must prepare for the contest. You will need to master mathematical concepts and refine your analytical skills. Secondly, dedication and strategic learning will develop the ability to approach problems methodically. As a result, you solve them efficiently within time constraints.
How to Prepare for Math Olympiad Questions?
Conceptual Learning
Firstly, you will need to understand fundamental concepts to build a strong mathematical foundation. Therefore, grasp core principles to solving complex problems. You can focus on math algebra, geometry, and number theory to enhance problem-solving skills. Also, practicing daily strengthens conceptual knowledge. You will recognize patterns and apply logical techniques to solve questions efficiently.
Next, you can review past math Olympiad questions to identify recurring patterns and question types. Solve previous problems to familiarize yourself with competition formats and improve accuracy. Analyzing solutions refines logical approaches and boosts confidence. Moreover, consistent exposure to various difficulty levels means you remain composed. At the same time, you solve unfamiliar problems under time constraints.
Speed practicing
Secondly, developing speed and accuracy is crucial for success. Timed practice enhances efficiency. It allows you to solve problems swiftly without compromising precision. Furthermore, you can set time limits to mimic real exam conditions. It will sharpen problem-solving techniques. Faster calculations and logical deductions help tackle challenging questions confidently.
Challenging yourself with math Olympiad questions strengthens mental agility and problem-solving capabilities. Furthermore, you can work on different question types that refine analytical thinking and enhance versatility. Identifying weak areas and focusing on targeted improvement ensures well-rounded preparation. You can practice problems to handle unexpected questions during the competition.
Problem-solving
Thirdly, you can use multiple problem-solving approaches to increase flexibility in tackling questions. Furthermore, exploring alternative methods helps develop a deeper mathematical understanding. Therefore, trying different techniques fosters creativity and improves logical reasoning. In short, experimenting with various strategies broadens analytical perspectives. As a result, you pick the most efficient solution method for each problem.
Applying diverse strategies to math Olympiad questions enhances problem-solving efficiency. Recognizing the best approach in different scenarios improves adaptability. In other words, you learn to switch methods when needed to optimize accuracy. Therefore, regularly testing multiple techniques sharpens decision-making skills. You develop a structured process when faced with unfamiliar or complex problems during the competition.
Group Study
Study groups offer many benefits. You can join a study group because it provides valuable peer insights and collaborative learning opportunities. Secondly, you can discuss concepts with others for deeper understanding. As a result, the study group exposes you to different problem-solving techniques. Also, group studies encourage critical thinking and allow knowledge sharing. You can engage with like-minded peers to create a motivating learning environment.
Practicing math Olympiad questions in a group setting enhances performance. You solve problems together. It introduces fresh perspectives and alternative methods. Also, discussing solutions helps refine logical reasoning and accelerates learning. Therefore, you can analyze different approaches to problem-solving strategies. In other words, it makes it easier to tackle difficult questions effectively during the competition.
Digital learning
Finally, you can utilize online resources and competition materials to expand your knowledge base. Video tutorials, problem-solving forums, and interactive quizzes help reinforce mathematical concepts. Modern students have access to various learning platforms that broaden their exposure to different problem types. Therefore, you can use digital tools to enhance self-paced learning. As a result, you can tailor it to your strengths and weaknesses.
Regularly attempting math Olympiad questions from online sources to improve adaptability. Interactive platforms offer real-time feedback to identify mistakes and refine approaches. Engaging with timed online quizzes simulates actual competition conditions. It improves speed and accuracy. Lastly, you can explore diverse question banks to practice various problem formats. It builds confidence before the competition.
Math Olympiad Questions 1
Exponents, also known as powers or indices, are mathematical operations that represent repeated multiplication. Subsequently, the numbers are multiplying with the base repeatedly. The math Olympiad questions today explore the principles and techniques in addition to shortcuts. As a result, you will solve exponent problems with ease and confidence. Here is a guide on how to solve exponential math during the exam.
2n-7. 5n-4 = 1250
First, we express 1250 in exponents. Therefore, the figure becomes 54. 2
As a result, we can rewrite the expression
2n-7. 5n-4 = 54. 2
Comparing elements on both sides of the equation
2n-7 = 21
We can cancel the bases.
N – 7 = 1
Therefore, n = 8
Secondly, we solve for 5.
5n-4 = 54
Therefore, n also equals 8.
Verification
2n-7. 5n-4 = 1250
28-7. 58-4 = 1250
2. 54 = 1250
2. 625 = 1250
1250 = 1250
Do you want to learn how to get a fraction of a number in a shortcut way? The guide to whole number fractions teaches you the solution in the easiest and shortcut way. As a result, you can solve math fraction problems in a few seconds for admission, bank, and, also, GRE exams.
Math Olympiad Questions 1
The Math Olympiad questions are a fascinating challenge in algebraic manipulation and problem-solving. The equations determine the value of 𝑥 that satisfies the equation. Thus, you can carefully apply mathematical principles and techniques. Furthermore, you become an expert in exponent rules, factoring, and algebraic manipulation. As a result, you unravel the solution to an intriguing problem. Let’s embark on this mathematical journey. You will learn about the secrets hidden inside the equation.
The equation is often part of math Olympiad questions. First, we have to figure out the bases before we can simplify the exponents. Next, you remove all of the equation’s common terms and elements. Finally, we need to reorder the elements and compute the natural logarithm of each side in order to find the value of x.
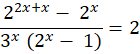
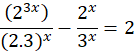
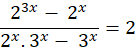
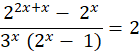
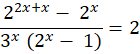
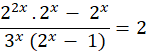
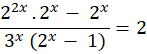
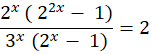
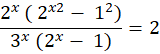
Since (a-b)2 = (a-b) (a+b). Therefore, the equation expands to
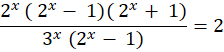
Next, we eliminate the common terms on the fraction
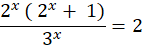
Now, we cross-multiply again to group the common terms
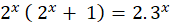
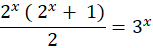
Finally, we input options into the equation to identify the common answer.
A = 2, so, if x = 2
2.5 = 9
10 does not equal to 9.
B = 1, so, if x = 1
1.3 = 3
3 =3
Are you ready to solve math Olympiad questions?
Preparing for the math Olympiad requires dedication, strategic practice, and continuous learning. Only then can you apply effective problem-solving techniques that sharpen logical thinking and analytical skills. Consistent practice strengthens confidence and adaptability. With structured strategies, you can review past questions and engage in collaborative learning. Email support@bornomalathebd.com to become part of a growing community.