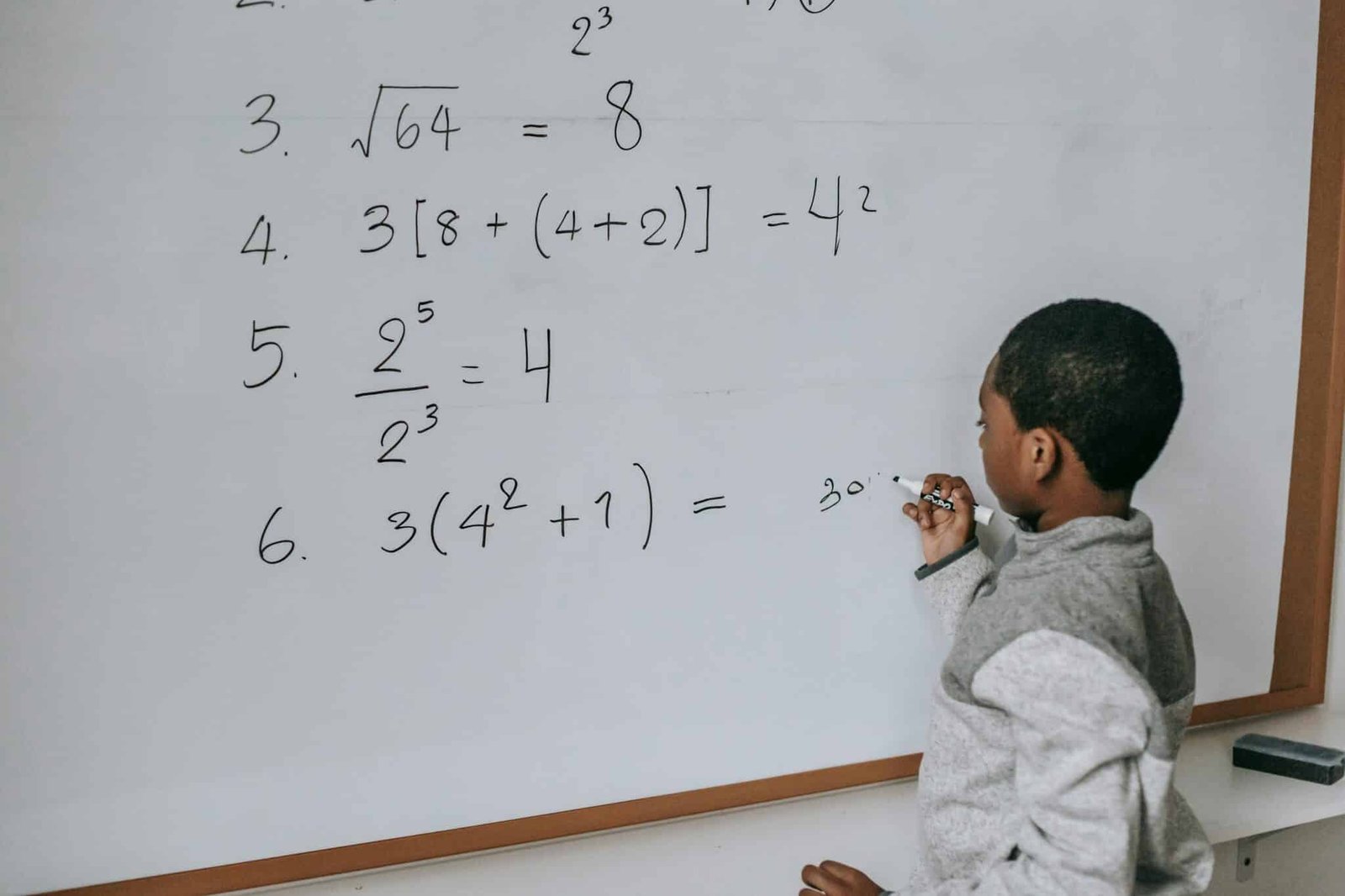Math Olympiad problems require deeper understanding and advanced problem-solving skills. Unlike regular questions, they demand creativity and logical reasoning. Therefore, participants must explore unconventional approaches. Furthermore, the challenges are intellectually stimulating. Consequently, math Olympiad problems encourage critical thinking. In addition, they bridge concepts across topics and foster innovative solutions. So, it sets them apart from traditional academic exercises.
How are math Olympiad problems different from regular questions?
Abstract Thinking in math Olympiad Problems
Firstly, math Olympiad problems emphasize abstract thinking. In other words, it distinguishes them from routine questions. Regular problems often focus on direct calculations. On the other hand, Olympiad questions require participants to identify patterns. They generalize results and construct arguments. In other words, it promotes mathematical insight.
Time Constraints in math Olympiad Problems
Secondly, math Olympiad problems test both accuracy and time management. While regular questions usually offer straightforward solutions, Olympiad problems involve multi-step reasoning within a limited time. Moreover, participants must evaluate their approach quickly. At the same time, you avoid errors. The combination of pressure and complexity sharpens problem-solving skills. It makes the challenges uniquely demanding yet rewarding.
Creativity in math Olympiad Problem Solving
Unlike standard questions, math Olympiad problems require creative approaches to unfamiliar scenarios. Participants must think beyond formulas and apply principles innovatively. As a result, the challenges encourage exploration. In other words, the students use unexpected methods that can lead to solutions. The emphasis on creativity nurtures flexible thinking and differentiates Olympiad problems from routine exercises.
Interdisciplinary Nature of math Olympiad Problems
Math Olympiad problems often integrate concepts from multiple mathematical areas. Unlike regular questions that focus on one topic, Olympiad challenges demand understanding across algebra, geometry, number theory, and combinatorics. The interdisciplinary nature enriches participants’ problem-solving abilities. Furthermore, it fosters connections between topics. Lastly, it enhances their appreciation for mathematics.
Math Olympiad Problems: 𝒙3+𝒙2 =1/8
Step 1: Rewrite the Original Equation
Firstly, we start with the given equation
8(x3 + x2) = 1
Then, we distribute 8 to both terms inside the parentheses:
8x3 + 8x2 = 1
Step 2: Test with a General Form
Subsequently, we adjust the coefficients and rewrite:
23x3 + 23x2 = 1
Therefore, it leads to testing a modified version:
(2x) 3 + 22+1 x2 = 1
Since the equation involves exponential terms, use the rule ax+y = ax. ay
Now, you can rewrite the equation as:
(2x) 3 + 22 . 21 x2 = 1
Next, you simplify further:
(2x) 3 + (2x)2. 21 = 1
(2x) 3 + (2x)2. 2 = 1
Step 3: Introduce a Substitution
Now, to simplify the equation, let m=2x. Next, we substitute m into the equation.
Therefore, m3 + 2m2 – 1 = 0
Step 4: Group and Factorize
Foremost, group the terms for easier factoring:
m3 + m2 + m2 – 1 = 0
Subsequently, you must group further:
(m3 + m2) + (m2 – 1) = 0
Next, you can factorize each group:
m2 (m+1) + (m+1) (m-1) = 0
You can combine terms:
(m+1) (m2+ m-1) = 0
Step 5: Solve for m
From the initial factorization, m+1 = 0
Since m=2x, substitute back to find x.
2x = -1
X = -1/2
Step 6: Solve the Quadratic Equation
Now, we use the quadratic formula to solve for m2+ m-1
Here, a=1, b=1, and c=−1. Next, you substitute the values:
Step 7: Back-Substitute to Solve for x
Have a look at the Final answer!
Math Olympiad problem x3−x2−20x=0
Initial Factorization
X (x2−x−20) = 0. Therefore, x equals to zero.
Step-by-Step Factorization of the Equation
Next, we will factorize the quadratic equation:
x2−x−20=0
Step 1: Identify the General Form
Subsequently, the equation is in standard quadratic form:
Here:
- Firstly, a=1. It is the coefficient of x2
- Secondly, b=−1. In other words, it is the coefficient of x,
- Lastly, c=−20 is the constant term.
Step 2: Find Two Numbers
Next, we can factorize to find two numbers:
- Multiply to a⋅ c= 1⋅ (−20) = -20
- Add to b=−1
The two numbers are 4 and -5 because:
4 ⋅ (−5) = −20 in addition 4+(−5) = −1
Step 3: Split the Middle Term
Now, we use the two numbers to split the middle term (−x):
x2−x−20=0
x2+4x−5x−20=0
Step 4: Group Terms
Next, we group the terms in pairs to factorize:
(x2+4x) − (5x+20) = 0
Step 5: Factor Out the Common Terms
Now, we factor out the greatest common factor (GCF) from each group:
x(x+4) −5 (x+4) = 0
Step 6: Factorize the Common Binomial
Now, factor out the common binomial (x+4):
(x+4) (x−5) = 0
Step 7: Solve for x
However, you must set each factor equal to zero:
- x+4 = 0 ⇒x= −4
- x−5 = 0⇒ x=5
Final Answer:
Therefore, the factorized form of the equation is:
(x+4) (x−5) = 0
The solutions are:
x=−4, 5, and 0
The Given Equation is x3−x2−20x=0
Step 1: Verify for x=−4
First, you substitute x= −4 into the equation:
(−4)3 − (−4)2 − 20(−4)
Calculate each term:
(−4)3= −64, (−4)2=16, −20(−4) = 80
Substitute the values
−64−16+80=0
Since the left-hand side equals 0, x= −4 is a solution.
Step 2: Verify for x=5
Secondly, you substitute x=5 into the equation:
(5)3−(5)2−20(5)
In the next step, you calculate each term:
(5)3=125, (5)2=25, −20(5) = −100
Subsequently, you substitute the values:
125−25−100=0
Since the left-hand side equals 0, x=5 is a solution.
Step 3: Verify for x=0
Lastly, substitute x=0 into the equation:
(0)3−(0)2−20(0)
Calculate each term:
(0)3=0, (0)2=0, −20(0) = 0
Substitute the values:
0 – 0 – 0 = 0
Since the left-hand side equals 0, x=0 is a solution.
Final Verification
Therefore, the solutions x= −4, x=5, and x=0 all satisfy the equation x3−x2−20x = 0
How to solve math Olympiad problems confidently?

Quadratic math Olympiad Equations
Foremost, to solve quadratic equations confidently in Olympiad problems, you must identify the correct approach using factoring. Subsequently, you can complete the square or the quadratic formula. However, always check for potential simplifications and verify solutions in the math Olympiad problems. In short, you develop clarity and accuracy for tackling complex math Olympiad problems.
Exponential Math Olympiad Solutions
Solving exponential functions in Olympiad math problems requires recognizing hidden patterns and applying logarithms effectively. First, you simplify expressions to isolate the exponent. Next, explore substitutions if needed. Moreover, you can test solutions according to logarithmic steps. Therefore, consistent practice and strategic thinking will ensure you confidently handle the math Olympiad problems.
Other Equations
For other math word problems, such as systems or polynomials, approach problems systematically. Foremost, you can eliminate variables or apply substitution. Moreover, simplify terms to reveal solvable structures. In addition, you can explore symmetry or graphing techniques for deeper insights.
Do not let math Olympiad problems intimidate you.
Lastly, you can master math Olympiad problems with persistence, creativity, and strategic thinking. As a result, you can explore diverse quadratics, exponentials, and polynomials equations. Embrace unconventional approaches so you build confidence and precision. Remember, practice and patience are essential for success.